PUMA - Rapid Enriched Simulation Application Development

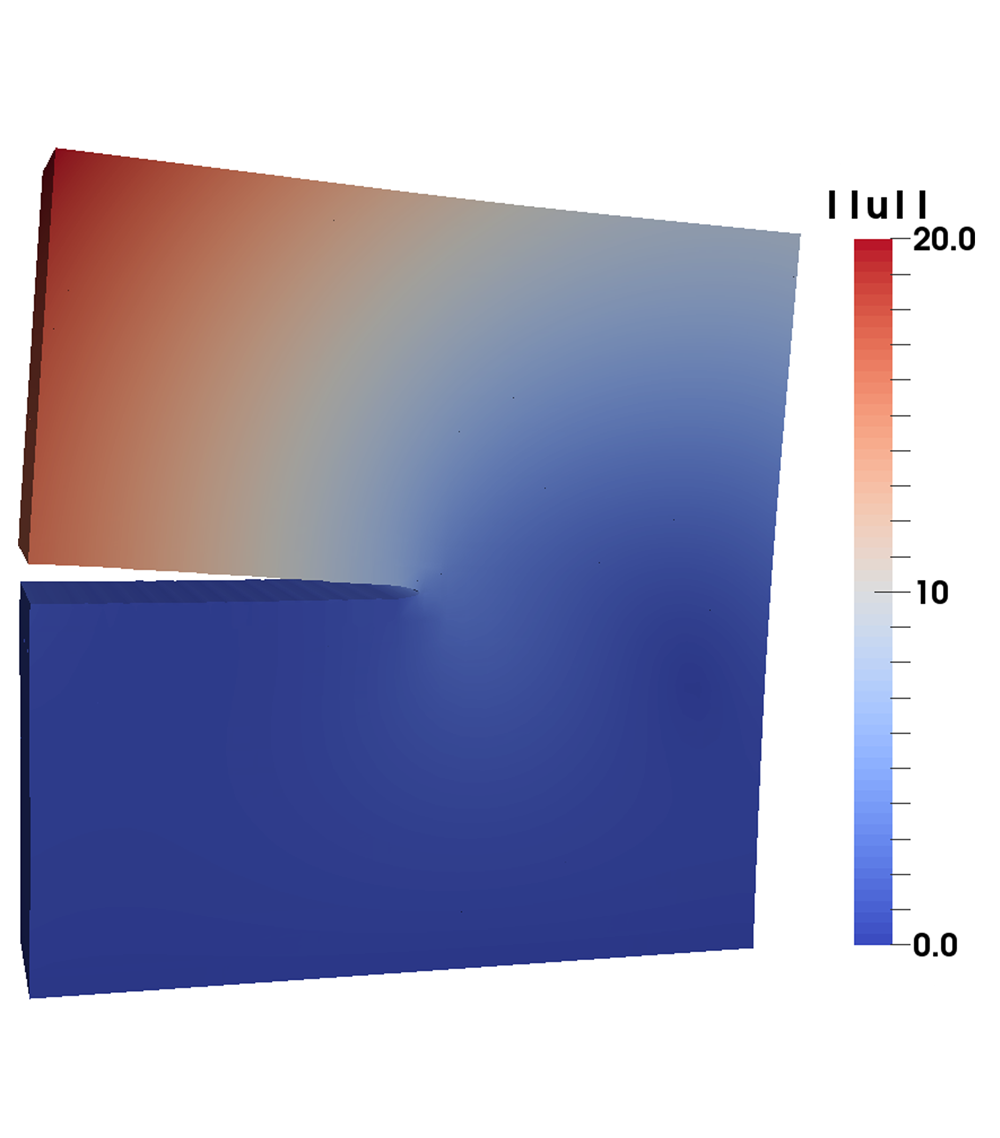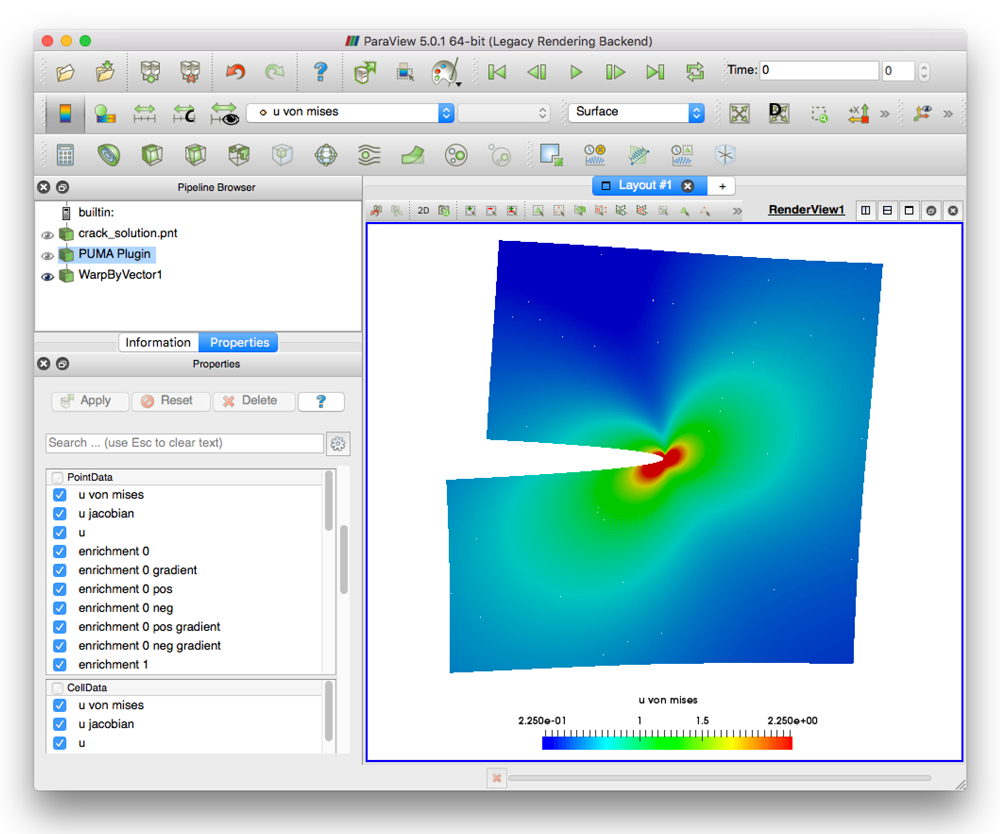
The PUMA software toolkit allows engineers to quickly implement simulation applications using generalized finite element techniques based on the partition of unity method (PUM). Compared to classical finite element methods (FEM), a PUM can directly utilize user insight, domain-specific information and physics-based basis functions in order improve the approximation properties of the model and to reduce the computational cost substantially. PUMA thus allows for the rapid evaluation of novel models.

An introduction to the PUM can be found in

M. A. Schweitzer. A Parallel Multilevel Partition of Unity Method for Elliptic Partial Differential Equations, Volume 29 of Lecture Notes in Computational Science and Engineering, Springer, 2003.

Using a multi-layered architecture, PUMA hides the internal methodological and implementation complexity from the user. The PaUnT module contains the computational core of the framework and provides platform independence, computational efficiency, and the possibility to interact with scientific third party libraries.

PUMA provides a Python interface which provides easy access to the higher level functionality of PaUnT. On the application level, the user implements the simulation application with the help of this interface, which allows to control all aspects of the method, but do not require the user to be aware of all details of the PUM or its implementation within the computational core of PUMA.

The GECO Python Front-End allows the user to specify mathematical expressions via PUMA's own expression language in a notation that is very close to typical mathematical formulations.

The GECO C++ Back-End ist the key component of PUMA's user interface. GECO (Generic Expression COmpiler) is an optimizing expression compiler. It operates on an abstract intermediate representation for mathematical expressions and includes code generators for PaUnT's weak formulations, enrichments, and general scalar/vector field expressions.

The ParaView Plugin integrates the powerful visualization and post-processing tool ParaView.

PUMA is particularly suitable for fracture mechanics problems. It is well known that such problems pose severe challenges for classical FEM. For example, the solution exhibits a discontinuity across the crack and is singular in the crack tip. In the PUM, these difficulties are rather simple to resolve by the use of available appropriate enrichment functions and suitable solution methods for the resulting systems of equations.